数据结构与算法

2021-01-03

数据结构与算法

绪论

算法

计算=信息处理

借助某种工具，遵照一定的规则，以明确而机械的形式进行。
计算模型 = 计算机 = 信息处理工具

算法：指的是在特定计算模型下，，旨在解决特定问题的指令序列。

输入	待处理的信息（问题）
输出	待处理的信息（答案）
正确性	的确可以解决特定的问题
确定性	任一算法都可以描述成为一个由基本操作组成的序列
可行性	每一个基本操作都可以实现，且在常数时间里面完成
有穷性	对于任何输入，经过又穷次数操作后，都可以得到输出

关于有穷性

$$
Hailson(n) =
\begin{cases}
{1} \ \ \ \ \ \ \ \ \ \ n \leq 1 \
{n}\ \cup \ Hailstone(n/2) \ \ \ n = 2K \
{n}\ \cup \ Hailstone(3n+1) \ \ \ n = 2K - 1
\end{cases}
$$

int Hailstone(int n)
{
    int length = 1;
    while (n != 1)
    {
        (n % 2) == 0? n = n/2 : n = 3 * n + 1;
        length ++;
    }
    return length;
}

关于这个Hailstone函数，我们输入的常数未必与我们的输出的结果成正比。

对于任意的n，我们都一定拿到有穷性的Hailstone长度吗！

所以说，上述的Hailstone是一个程序，不是一个算法。
$$
程序\neq 算法
$$

好算法

正确：符合语法，能够编译，链接。
- 能够处理简单的输入
- 能够处理大规模的输入
- 能够处理一般性的输入
- 能够处理退化的输入
- 能够处理任意合法的输入
健壮：能够辨别不合法的输入，且能够做适当的处理，也就是异常处理。
可读：结构化 +准确命名+注释+···
效率：速度尽可能的快，存储空间尽可能的少。

$$
\begin{matrix}
Algorithms + Data\ Structures = Programs \
(Algorithms + Data\ Structures)\times efficient = Computing
\end{matrix}
$$

计算模型

成本：运行时间 + 所需储存空间

不同的算法解决的问题规模不太相同，相同问题规模的算法计算成本大体差不多。

在考察算法的效率的时候，我们需要使用该算法解决问题的最坏的情况去描述这个算法的效率，也就是计算成本最高的情况。如前面的Hailstone，不可以找到最坏的情况，所以很难对这个算法提供一些描述性信息。

Turing Machine（图灵机）

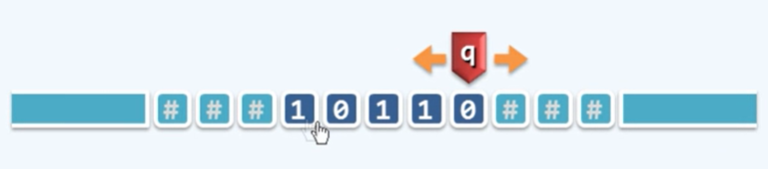
63__MXTY7I__@B_US0T1@_8.png

Tape: 依次均匀的划分单元格，各注有一段字符，默认为‘#’
Alphabet 字符的种类有限
Head 总是对准某一个单元格，并且可以读取和改写其中的字符，每经过一个节拍，可转向左侧或者右侧。
State TM总是位于有限种状态中的某一种状态，每次经过与1个节拍，可以安好规则转向另外一种状态。
Transition Function： (q, c; d, L/R, p)
- q为读写头
- c为被读取的字符
- d为即将替换成为的字符
- L/R为转换方向
- p为状态，如果为h则图灵机终止

RAM: Random Access Machine

寄存器顺序编号，总数没有限制

R[0], R[1], R[2], ...

每一项基本操作仅仅需要常数时间

1
2
3

R[i] <- c				R[i] <- R[R[j]]		R[i] <- R[j] + R[k]
R[i] <- R[j]			R[R[i]] <- R[j]		R[i] <- R[j] - R[k]
IF R[i] = 0 GOTO 1		IF R[i] > 0 GOTO 1	GOTO 1        STOP

与TM模型一样，RAM模型也是一般计算工具的简化与抽象使得我们能够在独立的平台上进行比较与评判
- 算法的运行时间取决于算法需要执行的基本操作的次数
- T（n） = 算法为求解规模为n的问题所执行的基本操作次数

大o记号

渐进分析法：大o记号

Asymtotic analysis 当n >> 2 之后，对于规模为n的输入，算法

所需要的基本操作次数： T（n） = ?
需要占用的存储单元数： S（n） = ?

Big-o notation
$$
\begin{matrix}
大o记号（big-o notation）\
使用放缩的方法取得最高次项，忽略常数
\end{matrix}
$$
Big Ω 在特殊的情况下会考虑这些其他的分析法。

分类

o(1): 这类算法的效率最高，在不含调用，不含循环，不含转向的大部分都是o(1)级别的算法。
o(logn):
- 对数中不在标明底数，经过对数变换后始终能转换底。常系数忽略。
- 对数中指数幂次项不影响o的次数，指数可以提出来作为常数
- 指数多项式仍然找到最高次项作为o
o(n ^ c):
- 找到最高次项的复杂度
- o(n)线性复杂度，已经可以是非常满意了。

o(2 ^ n) ：指数复杂度

只要我们的常数是大于1的，则认为这个是很难以解决的。

// 难解
#include <iostream>
int fnt(int number)
{	
    if (number == 1 || number == 0)
    {
        return 1
    }
    return fint(number - 1) + fint( number - 2);
}
// 多项式复杂度
unsigned long int fib2(unsigned int number)
{
    unsigned long int result = 0;
    unsigned long int a = 1;
    unsigned long int b = 1;
    int count = 2;
    if (number == 1 or number == 2)
    {
        return 1;
    }
    else{
        while (count < number)
        {
            result = a + b;
            b = a;
            a = result;
            count ++;
        }
        return a;
    }

}

Subset
- [问题描述]
  - S包含n个正整数， Σs = 2m
  - S是否有子集T，使得∑T=m？
- 这个问题就是我们所说的NP-C问题，遍历所以有的结果才能得出想要的解。
不存在多项式优化解，只能使用最差的解，也就是遍历。（？？？）

算法分析

$$
两个主要任务= 正确性（不变性\times 单调性）+ 复杂度
$$

C++等高级语言的基本指令，均等效于常数条RAM的基本指令；在渐进下，二者的效果大抵相同。
- 分支转向： GOTO
- 迭代循环： for(), while() //本质上是 IF goto
- 调用 + 递归 //本质上都是goto
复杂度分析的主要方法：
- 迭代：级数求和
- 递归：递归追踪 + 递推方程
- 猜测 + 验证

级数

算数级数：与末项平方同阶

$$
T(n) = 1+2+3+4+ \dots + n= \frac{n(n+1)}{2}=O(n^2)
$$

幂方级数：比幂次方高一阶

$$
\sum_{k=0}^{n}k^d \approx \int_{0}^nx^{d}dx=\frac{1}{d+1}x^{d+1}|_{0}^{n}=\frac{1}{d+1}n^{d+1}=O(n^{d+1})
$$

几何级数：
从某项开始复杂度都呈现倍数的增长。（等比数列，或者类等比数列）
收敛级数：
$$
例1： 1 + \frac{1}{2^2}+\dots + \frac{1}{n^2} < 1 + \frac{1}{2^2}+\dots = \frac{\pi^2}{6}=O(1)
$$

$$
例2:\frac{1}{3}+\frac{1}{7}+\frac{1}{8}+\frac{1}{15}+\dots =1=O(1)
$$

调和级数

$$
h(n)=1 + \frac{1}{2}+\frac{1}{3}+ \frac{1}{4}+\frac{1}{5}+\dots=\Theta(logn)
$$

对数级数

$$
log1 + log2 + log 3 + \dots + logn=log(n!)=\Theta (nlogn)
$$

循环

算数级数：

$$
算数级数： \sum_{i=1}^{n}k=1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2}=O(n^2)
$$

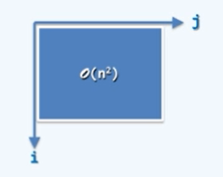
![KKPR__D`F08_TWY_S7D_YIJ.png](https://i.loli.net/2021/01/02/Z3FhknW6KOdPJRU.png)

几何级数：

void geometricSeries(int n)
{
    for (int i = 1; i < n; i <<= 1)
    {
        for (int j = 0; j < i; j ++)
        {
            cout << j << endl;
        }
    }
}
/*
输出结果： 
0, 0 1, 0 1 2, 0 1 2 3, 0 1 2 3 4, 0 1 2 3 4 5 ......
*/

$$
几何级数： 1 + 2 + 4 + \dots + 2 ^ {[log_2(n-1)]}=\sum_{k=0}^{|log_2(n-1)|}2^ {log_2i}=2^{|log_2n|}-1 = O(n)
$$

这是由于 i 的增长是几何递增的，当几何增长到n时，增长的次数是log的形式，只有这样，才能算出来是几何指数。

如果说单纯的几何级数，不是这种限定条件的话，就会使几何级数递增。

for (int i = 0; i <= n; i ++)
{
    for (int j = 1; j < i; j <<= 1)
    {
        cout << j << endl;
    }
}

$$
\begin{align}几何级数：分析：由于内部增长过快，导致有时候外部循环的增长不能满足内部，也就是说存在\
有些i会得到相同的输出次数，这也就是内部的增长速度限定外部的打印次数的情况。这也就变相导\
致模型的复杂度是O（logn * 2 ^ {logn}）
\end{align}
$$

冒泡排序

代码：

void bubblesort(int input[], int length)
{
    bool flag = true;   // 初始化一个布尔变量帮助我们判断是否排序完成
    while (flag)
    {
        flag = false;   // 初始化为false 认定这是一个未排序的序列
        for (int i = 1; i < length; i ++)
        {
            if (input[i - 1] > input[i])   // 出现前面的大于后面的则把后面的与前面的交换
            {
                swap(input[i - 1], input[i]);    //交换
                flag = true;   // 把flag变成true 是由于这个排序出现了逆序的，需要再检查一遍
            }
        }
        length --;   // 长度减一，由于在经历上面一次循环之后最大值已经被放在最后一位了无需检查最后一位。
    }
    // 打印模块
    for (int i = 0 ; i < 10; i ++)
    {
        printf("%d\n", input[i]);
    }
}
/*
	知识点： 
		1.使用布尔变量作为判断跳出循环的条件，避免了重复检查的资源浪费。
		2.先设置为false是怀疑论的基本操作，始终坚信这个输入者是不会给我们排好序的数组的
		3.swap函数交换的是地址，不可以填入数值
*/

$$
\begin{matrix}
在冒泡排序中，用最坏的来预测这个算法的复杂度，也就是完全逆序，\
T(n)= n + (n-1)+ \dots + 1 = \frac{n(n+1)}{2}=O(n^2)
\end{matrix}
$$

封地估算

$$
\begin{matrix}
时间估计: \
1d = 10 ^ 5 sec \
100Y = 3 \times 10 ^ 9\
300Y \approx 10^{10}
\end{matrix}
$$

迭代与递归

迭代

Decrease-and-conquer

为了求解一个大问题，可以
- 将其划分为多个小问题
- 分别求解子问题
- 合并所有子问题的解，得到原来问题的解

Divide-and-conquer

为了求解一个大规模的问题，可以
- 将大问题划分为若干的子问题，规模大致相当
- 分别求解子问题的解
- 由子问题的解得到原问题的解

递归方程

$$
T(n)=T(n-1) + O(?)\
T(1) = ？\
综合判断这个递归效果究竟如何？
$$

数组倒置

递归代码：

void seqReverse(int *head, int start, int end) {
    if (start < end) {
        swap(head[start], head[end]);
        seqReverse(head, start + 1, end - 1);
    }
}

迭代版本代码：

void seReverse(int * head, int start, int end) {
    for (int i = 0; i < (start + end) / 2; i ++, start ++, end --) {
        if (start < end) {
            swap(head[start], head[end]);
        }
        else {break;}
    }
}

迭代版本的与递归版本的时间复杂度都是O（n）基本差不了太多。

二分递归

int sum(int *list, int begin, int end)
{
    if (begin == end) {
        return list[end];
    }
    else {
        int mid = (begin + end) / 2;
        return sum(list, begin, mid) + sum(list, mid + 1, end);
    }
}

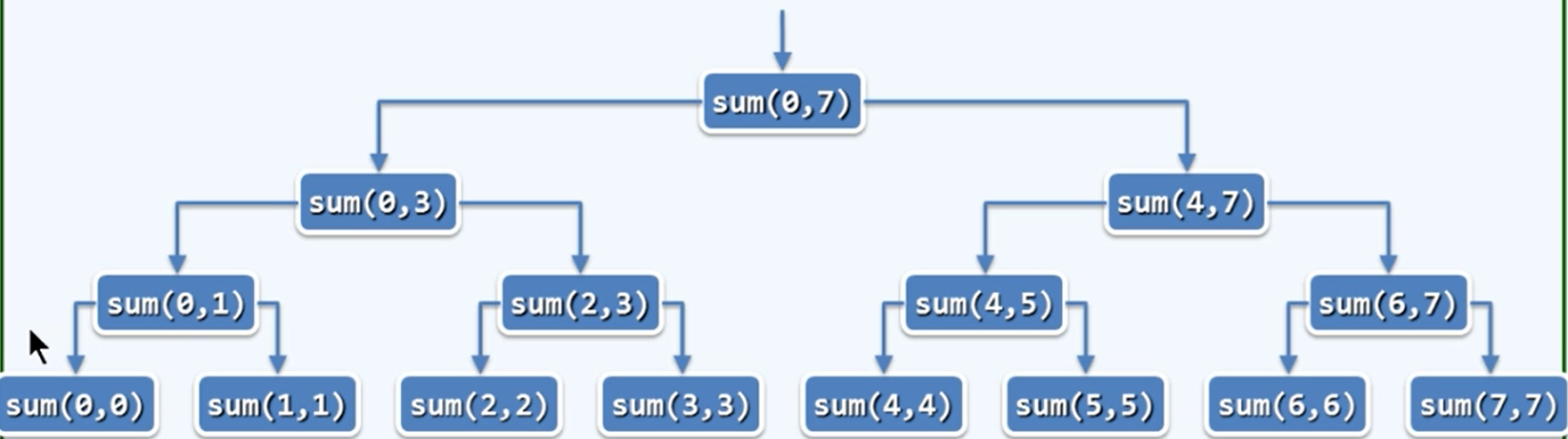
P7I8Y9`528BT_`UIXN7_R_C.png

递归分析

首先各层是2的倍数，但是被总数n制约

$$
T(n) = O(1)(2^0 + 2^1 + 2^2 + \dots + 2^{logn})\
T(n) = O(1) \times O(n)=O(n)
$$

制约的最高层数

$$
由于最后一层是所有元素：故最后一层为n\
那么设这第i层\
2^i=n \Rightarrow i=logn \
这也就是为什么最后一层为 2^{logn} 的原因
$$

递推方程

$$
T(n) = 2T(n/2) + O(1)\
T(1) = O(1) \
求和最后得到的还是O（n）
$$

Max2

从数组A中找到最大的两个值，并且返回其下标

解法一：蛮力划分区找最值

void max2(int *list, int lo, int hi, int x1, int x2) {
    int x21, x22 = lo;
    for (int i = lo; i < hi; i++) {
        if (list[x1] < list[i]) {
            x1 = i;
        }
    }// 第一层找到最大值
    for (int i = lo; i < x1; i++) {
        if (list[x21] < list[i]) {
            x21 = i;
        }
    }// 在余下两个区间里面找到次大值
    for (int i = x1 + 1; i < hi; i++) {
        if (list[x22] < list[i]) {
            x22 = i;
        }
    }
    x2 = list[x22] > list[x21] ? x22 : x21;// 比较赋值
    cout << list[x1] << endl;
    cout << list[x2] << endl;
}

解法二：动态的构建一个数组存放两个下标

void max2Two(int *list, int lo, int hi, int x1, int x2) {
    int *tamp[2] = {&x1, &x2};
    for (int i = lo; i < hi; i ++) {
        if (list[x1] < list[i] && list[x2] < list[i]) {
            x2 = x1; 
            x1 = i;
        }
    }
    for (int* & i : tamp) {
        cout << list[*i] << endl;
    }
}

x1负责去找最大值，当找到新的最大值之后丢给x2这样就总能够保证x2比x1小了。

解法三：二分递归

void max2(int list[], int lo, int hi, int &x1, int &x2) {
    // 搭建递归基底， 最终的一项总是以2，或者3个元素组成的一个小数组。
    if (lo + 3 == hi) {
        for (int i = lo; i < hi; i++) {
            if (list[x1] < list[i]) {
                if (list[x2] < list[i]) {
                    x2 = x1;
                    x1 = i;
                }
            }
        }
        return; // 一定得由返回值信息， 不论返回的是什么，不然又会继续走下去了。无限递归。
    } // 当余下为3的时候找出最大值与次大值，
    if (lo + 2 == hi) {
        x1 = list[lo] > list[lo + 1] ? lo : lo + 1;
        x2 = (lo + lo + 1) - x1;
        return;
    } // 当余下为2时候给给这两个值排个序。
    int mid = (lo + hi) / 2; // 获取中间值
    int x1L, x2L = 0; // 创建左边数组的两个输出参数
    max2(list, lo, mid, x1L, x2L);
    int x1R, x2R = 0;
    max2(list, mid, hi, x1R, x2R);
    if (list[x1L] > list[x1R]) {
        x1 = x1L;
        x2 = (list[x2L] > list[x1R]) ? x2L : x1R;
    }
    if (list[x1L] <= list[x1R]) {
        x1 = x1R;
        x2 = list[x2R] > list[x1L] ? x2R : x1L;
    }
}
/*
	递归总结：
    	1. 构造递归的时候只需要抓住前后两项之间的关系就可以了，这样递归就有了雏形。
    	2. 递归最重要的是跳出递归的方式，也就是要设置好递归基，不能形成无限深度度的递归。
    	3. 不论是什么递归，都得有返回值，也就是返回递归的结果，否则会形成无限递归。
    	4. 引用类型的传参是非常好用的，可以直接改变数据的真实值，而不去另加创造，节省了内存的使用，在当输出结果是不断变化，且结果正式这个的时候，向函数引入这这样的参数类型是非常高效的。
*/

$$
由于使用了二分递归，这个算法的复杂度达到目前最低。\Theta（n） = \frac{5}{3}n -1
$$

动态规划

$$
Make\ \ it \ \ work, \
make \ \ it \ \ right, \
make \ \ it \ \ fast. \
-Kent \ \ Beck
$$

所谓动态规划就是使用递归解决之后，找到对应的迭代形式。

最长公共子序列 (subsequence)

解法一：递归求解

1	//待完成，我感觉递归真的做出来就是憨憨，超级麻烦

解法二：动态规划，迭代求解。

void lcs(string str1, string str2, int **&m) {
    int lengthstrL = str1.length();
    int lengthstrR = str2.length();
    for (int count = 0; count < lengthstrL + 1; count ++) {
        m[count] = (int *) malloc((lengthstrR + 1) * sizeof(int));
        for (int j = 0; j < lengthstrR + 1; j++) {
            m[count][j] = 0;
        }
    }
    // 创造空间供给使用。
    // 初始化这个矩形字符图
    // 初始化为0

    for (int i = 1; i < lengthstrL + 1; i++) {
        for (int j = 1; j < lengthstrR + 1; j++) {
            //开始检索信息
            if (str1[i] == str2[j]) {
                m[i][j] = m[i-1][j-1] + 1;
            } else {
                if (m[i - 1][j] == m[i][j - 1]) {
                    m[i][j] = m[i - 1][j];
                } else {
                    m[i][j] = m[i - 1][j] > m[i][j - 1] ? m[i - 1][j] : m[i][j - 1];
                }
            }
        }
    }
}
/*
	总结：
		1. 引用类型的使用是 数据类型（data type） &  <variable name>
		2. 对于数组来看，c++可以制造多维数组，只要你想。
		3. malloc 好像可以直接用？好像确实可以。
		4. 注意分配内存，不然容易报错。
		5. 定义指针的时候让它等于空指针 nullptr
*/

所以说动态规划的核心就在于使用递归找出合理解法之后，使用迭代去描述这个算法，得到一个更加高效的解。

向量(Vector)

抽象数据类型 = 数据模型 + 定义该模型上的一组操作

抽象定义外部的逻辑特性操作&语义

一种定义不考虑时间复杂度不涉及数据的存储方式
数据结构 = 基于某种特定语言，实现ADT的一整套算法

具体实现内部的表示与实现完整的算法

多种实现与复杂度密切相关要考虑数据的具体存储机制

向量ADT

从数组到向量

引入，c或者c++中的数组都是一个个的物理地址与对应的值所组成的，而这个地址又可以写成线性的形式.

$$
A[i]的物理地址=A + i\times s
$$

s是该种数据的空间大小，所以我们又把数组叫做线性数组（Linear array）

向量
- 向量是数组的抽象与泛化，由一组元素按照线性次序封装而成
- 各个元素与[0, n)内的秩（rank）一一对应
- 元素的类型不受限制
- 操作简单，维护容易，安全，统一。
- 方便实现更加复杂的数据结构的定值
向量ADT接口

操作	功能	适用对象
size()	报告向量当前的规模（元素总数）	向量
get(r)	获得秩为r的元素	向量
put(r, e)	用元素e替换秩为r的数值	向量
insert（r, e）	e作为秩为r的元素插入，原后继元素往后推移	向量
remove（r）	删除秩为r的元素，返回该元素中原本存在的对象	向量
disordered（）	判断是否所有元素已经是非降序排列了	向量
sort（）	调整所有元素的未知，使之按照非降序排列	向量
find（e）	查找目标元素e	向量
search（e）	查找目标元素e，返回不大于e且秩最大的元素	有序向量
deduplicate（）	剔除出重复元素	向量
uniquify（）	剔除重复向量	有序向量
traverse（）	遍历向量并且统一处理向量中的元素，处理方法由函数对象指定	向量

构造与解析

Vector模板类

typedef int Rank; // 秩
#define DEFAULT_CAPACITY 3 //默认初始容量（实际应用中偏大）
template <typename T> class Vector {
    private: Rank _size; int _capacity; T* _elem; //规模，容量，数据区
    protected:
    /* 内部函数 */
    public:
    /*构造函数*/
    /*析构函数*/
    /*只读接口*/
    /*可写接口*/
    /*遍历接口*/
    /*。。。。*/
}
/*
	总结： 
		1.前下划线为私有变量的声明
*/

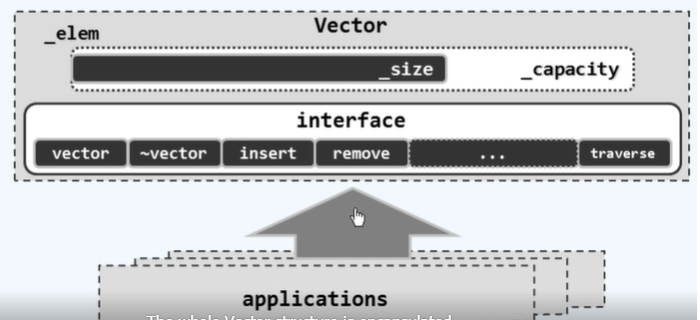
_Y1@Z09K_WV_M3__WK@YMR4.png

//构造与析构
Vector(int c = DEFAULT_CAPACITY)
{_elem = new T[_capacity = c]; _size = 0;} //默认
//创建一个大小为c的空间去存储，初始化的_size=0
Vector(T const * A, Rank lo, Rank hi)
{ copyFrom(A, lo, hi);}
//从数组的lo到hi复制为一个新的向量
Vector(Vector<T> const& V, Rank lo, Rank hi)
{ copyFrom(V._elem, lo, hi)}
//从向量区间中复制
Vector(Vector<T> const& V)
{ copyFrom(V._elem, 0, V._size)}
//从向量整体复制
~Vector() {delete [] _elem; }
//直接释放掉内存空间。

复制

template <typename T> //T为基本数据类型，或者已经重载的复制操作符 “=”
void Vector<T>::copyFrom(T* const A, Rank lo, Rank hi) {
    _elem = new T[_capacity = 2 * (hi - lo)];
    _size = 0;
    while (lo < hi) //A[lo, hi)内的元素逐一复制
        _elem[_size++] = A[lo++]; //复制元素
}
/*
	总结: 
		1. template 是类模板，后面使用的T是代指各种不同的数据类型
		2. ::是域解析操作符，规定命名空间的namespace的
		3. 定义为const是为了防止被改变的风险。
*/

可扩充向量

静态空间管理策略

开辟内部数组_elem[]并使用一段连续的物理空间
- _capacity : 总容量
- _size : 当前实际规模n
若采用静态空间管理策略，容量_capacity固定，则有明显不足
1. 上溢（overflow）: _elem[]不足以存放所有的元素，尽管这时候系统还有足够的空间。
2. 下溢（underflow）： _elem[]中的元素少

$$
装填因子(load\ factor)\ \lambda = \frac{_size}{_capacity}\ <<\ 50%
$$

更加糟糕的是，一般应用环境难以精准预测空间需求量。

动态空间管理策略

在即将发生上溢的时候，适当扩大内部数组的容量，使之能够容纳新的元素。
- 当检测到即将溢出的时候把原来的copy到新的空间中，并且把原来的释放。

template <typename T>
void vector<T>::expend() {
    if (_size < _capacity) {
        return; // 如果说内部的存储量小于_capacity,则直接返回.
    }
    _capacity = max(_capacity, DEFAULT_CAPACITY);
    T* oldElem = _elem; // 指向老指针中的元素
    _elem = new T[2 * _capacity]; // 扩大容量
    // 转移操作
    for (int i = 0; i < _size; i++) {
        _elem[i] = oldElem[i]; 
        // 为什么oldElem中可以放下呢，这是由于传入的_elem其实是一个类似于数组的东西，
        // 如果不能就早就Significant Fault
        // 而我们不确定这个放入构造的向量能否存起来这么些数据。
    }
    delete [] oldElem; // 释放
}

扩容方法

递增式扩容

T* oldElem = _elem; _elem = new T[_capacity += INCREMENT]
最坏的情况下每次都要花时间进行扩容

$$
T(n)=1+2+\dots+n=\frac{n(n+1)}{2}=O(n^2)
$$

显然就单单花在扩容上的时间成本消耗就很大。

加倍扩容

T* oleElem = _elem; _elem = new T[_capacity * 2]
最坏的情况是：在初始化为1的满向量中连续的插入n = 2^m >> 2 个元素
于实在第1，2， 4， 8， 16。。。次需要扩容
在各次插入时候的复制元素的时间成本是

$$
1 + 2 + 4 + 8 + 2 ^m = O(2^{logn})= O(n)
$$

这种扩容方法相比于递增式扩容方法会降低时间成本。
- 这里的实际上就是几何级数，由于空间的大小2^m限制了的增长。
- 每次都又多余的空间被创造出来。

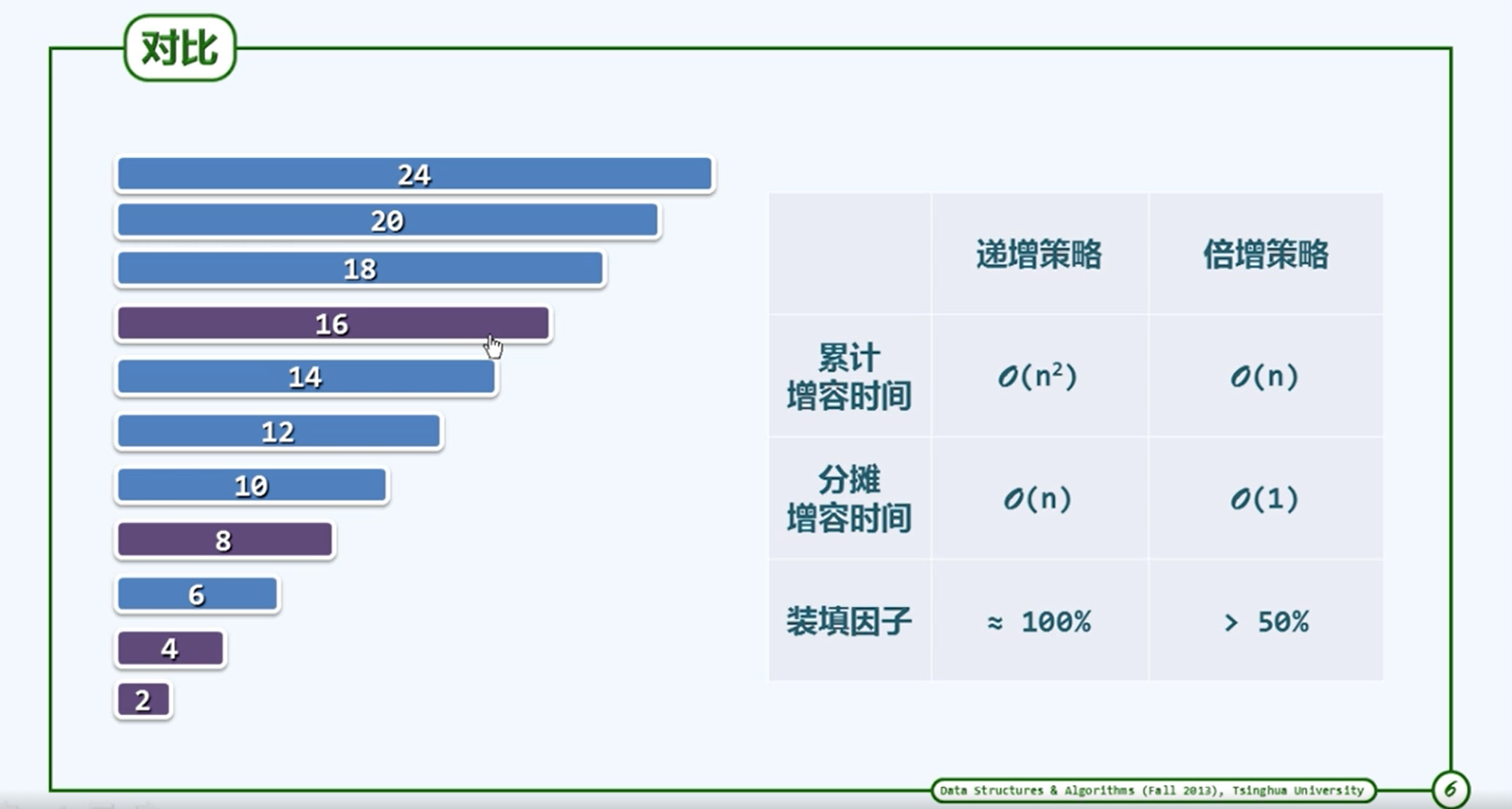
L_XBB3UQ_C_@JMRYED_JZM3.png

倍增的是在空间上做出了牺牲使得时间成本下降。

分摊复杂度

平均复杂度或者说期望复杂度（ average complexity ）

根据数据结构各种操作出现的概率的分布，将对应的成本加权平均

各种可能的操作，作为独立的时间分别考察

割裂了操作之间的相关性和连贯性

往往不能准确评估数据结构和算法的真实性能
分摊复杂度（ amortized complexity ）

对数阶结构连续地实施足够多次的操作，所需要的总体成本分担至单次操作

实现了对于数据结构与算法的整体考察

更加忠实的刻画了整体

更真实的反映数据结构与算法的效率

无序向量

元素访问

template<T>
T &vector<T>::operator[] (Rank r) const {
    // 注意这里的入口参数r需要是小于 _size的
    return _elem[r];
}
// 操作符的重载，返回值为_elem[r]
// 注意引用方法，所以这个访问方式使得我们可以赋在左边去访问。

插入

template<T>
Rank vector<T>::insert(Rank r, T & e) {
    expand();
    for(int i = _size; i > r; i--) {
        _elem[i] = _elem[i-1];
        // 这里的_size是相比于下标大一个单位的数字，所以可以直接这么写。
        // 通过这个把所有的数字都往后移动了一位
    }
    _elem[r] = e; // 在r位置上输入e
    _size ++;
    return r; // 返回秩
}

区间删除

template<typename T>
int vector<T>::remove(Rank lo, Rank hi) {
    if (hi == lo) { return 0; }
    while (hi < _size) {
        _elem[lo++] = _elem[hi++];
        // 赋值操作 一定得是从低位赋值开始，
        // 如果不是从低位开始，就容易出现我们高位数覆盖掉lo以下的数字，
        // 使用hi ++ 限定条件是 hi < _size 使得我们能够把所有的hi以后的数字完全遍历到，并且赋值成功。
    }
    _size = lo;   // 按理来说应该是 _size = _size - (hi‘ - lo’) 而这里的hi‘已经等于_size了， 而 lo' 已经变成了数组的长度
    return (hi - lo);  // 返回区间的长度
}

单元素删除

template<typename T>
T vector<T>::remove(Rank r) {
    T e = _elem[r]; // 备份一份元素以便于等会儿返回
    remove(r, r + 1);
    return e;
    // 颠倒过来使用单个元素去达到删除区间的作用是很不合理的
    // 每每调用一次删除元素，后面的元素都需要往前移动一位，这样就造成了复杂度的攀升
    // 因此我们应当使用区间删除去对应的做到删除元素的功能。
}

查找

template<typename T>
Rank vector<T>::find(const T &e, Rank lo, Rank hi) {
    while (lo < hi-- && _elem[hi] != e) {
        // 先判断lo 小于 hi ，然后hi --
        // 逐个扫描
    }
    return hi;  // 找到了 返回 hi。 // 如果合法的话就是我们的真实的秩，如果不是合法的话就返回一个小于lo 的函数
}

唯一化

在这个列表的前面开始查找，如果有重复的就剔除，使用remove函数，如果不行则继续下一个。

template<typename T>
int vector<T>::deduplicate() {
    // 在定义一个区间后在原先的区间去查找，如果找到了，就使用remove去掉这个元素，没有的话就往下去寻找。
    // 返回值是删除的重复元素的个数
    int oldSize = _size; // 记录下oldSize
    Rank i = 1;  // 从i=1开始查找。
    while (i < _size) { // 知道检测到最后一个元素
        (find(_elem[i], 0, i) >= 0) ? remove(i) : i++;
        // 如果数据合法的话就返回的秩是大于lo的，那么也就是说 >= 0 那么就找到了重复的数，那么remove（i）,否则就i ++
    }
    return oldSize - _size;  // 返回差值， 返回这个重复的元素的个数。

}

但是值得注意的是：这个方法的复杂度分析

$$
\begin{matrix}
算法的复杂度累计在while函数，与find与remove函数中\
累积起来的复杂度是O(n^2)
\end{matrix}
$$

遍历操作

遍历操作，统一对各个元素进行visit操作

使用函数指针

template <typename T>
void vector<T>::traverse(void (*visit)(T &)) {
    for (int i = 0; i < _size; i ++) {
        visit(_elem[i]);
    }
}
// 这个函数只能是那种没有返回值的那种函数

使用函数对象机制，可以做到全局性修改

template <typename T> template<typename VST>
void vector<T>::traverse(VST& visit) {
    for (int i = 0; i < _size; i ++) {
        visit(_elem[i]);
    }
}
// VST 理解为函数的模板，可以使得可以接受各种各样的函数

template<typename VST>
    void traverse(VST &visit) {
        for (int i = 0; i < _size; i++) {
            visit(_elem[i]);
        }
    }
// 遍历函数，传入的是一个函数，

    struct Increase {
        virtual void operator()(T &e) {
            e++;
        }
    };
// 函数对象，重载了（）操作符，使得可以用函数的方法进行访问。
    void increase(vector<T> & V) {
        V.traverse(Increase());
    }
    // 传入一个函数进去进行依次操作。

有序向量

有序性

$$
\begin{matrix}
无序向量 = 需要比对\
有序向量 = 需要比较大小\
\end{matrix}
$$

template<typename T>
int vector<T>::disordered() const {
    int count = 0;
    int i = 1;  // 开始阶段
    while (i < _size) {
        count += (_elem[i - 1] >= _elem[i]);
        i ++;
    }
    return count;
}
// 当一个向量的逆序数是0的时候这个向量就是有序的

唯一化

template<typename T>
int vector<T>::uniquify() {
    int oldSize = _size;
    int i = 0; // 从一号元素开始查重
    // 注意这里是正对有序向量而言的唯一化
    int j = 0;
    while (++j < _size) {
        if (_elem[i] < _elem[j]) {
            remove(i+1, j); // 删除掉这个区间的量， 但是我们还可以使用赋值去默认删除。
            i = j;
        }
    }
    return oldSize - _size;
}

二分查找

语义约定
- 至少有利于自身的维护， v.insert(1 + v.search(e), e)
- 即使是失败了也得给新元素提供参考
- 允许重复元素，则每一组也需要按其插入的次序排列
约定：在有序向量区间v[lo, hi)中，确定不大于e的最后一个元素
- 若e小于v[lo]，则返回lo - 1
- 若e大于v[hi - 1] 则返回hi - 1

template<typename T>
Rank vector<T>::binarySearch(T *A, T &e, Rank lo, Rank hi) {
    while (lo < hi) {
        int mi = (lo + hi) / 2;
        if (A[mi] < e) {
            lo = mi + 1;
        } else if (e < A[mi]) {
            hi = mi;
        } else {
            return mi;
        }
    }
    return -1;
}
// 根据二分类去寻找一个查找有序向量中的那个元素。
// 找不到的话就返回一个 -1

FibonacciSearch

//代码待实现

template <typename T>
Rank vector<T>::binarySearch(T *A, T &e, Rank lo, Rank hi) {
    Rank mi = 0;
    while (lo < hi) {
        mi = (lo + hi) / 2;
        (e < A[mi]) ? hi = mi : lo = mi + 1;
        /*
         * 区间压缩理解：
         *  1. 当满足e < A[mi] 时候，也就是说mi那个位置是严格大于我们的e的，也就是直接压缩过来
         *  2. 当不满足 e < A[mi] 的时候， 也就是说，mi那个位置一定是小于等于e的，那么我们就需要把这个区间往mi的右侧压缩
         *  如果等于e，那么往右压缩可以跳出重复项，如果不等于而是小于，那么就更加显然了，肯定得右移，如此以往最后得到的就是
         *  大于等于e的最右边的一个值，右边就是刚好大于e的值，而此时的lo是和hi相互重合的一个，往左走一格就是那个刚刚好小于e的位置
         *  然后返回值就是 --lo
        */
    }
    return --lo;
}

向量完全体

//
// Created by HP2 on 2021/1/4.
//

#ifndef DATA_STRUCTURE_AND_ALOGTHM_VECTOR_H
#define DATA_STRUCTURE_AND_ALOGTHM_VECTOR_H
/*
    总结：
        1. 函数声明需要在类的内部进行声明，然后可以选择性的在外面或者是在类的内部写函数体
        2. template是模板类，方便避免重载，那样写操作太复杂，是一种简化方法。
        3. typedef int Rank 是给int一个新的名字叫做Rank,实际上的效果是一模一样的。
        4. 自增自减运算符在前面的是先自增自减运算，然后再进行其他的操作。
        5. 析构函数无需在前面加上一些数据类型去限定返回值，
        6. 直接书写vector<T>才能表示这是一个类，这是由于定义这个类的时候就是在template模板下定制的
 */
#include <iostream>

using namespace std;
typedef int Rank;
#define DEFAULT_CAPACITY 5     //默认的容量大小

template<typename T>    //定义模板类

class vector {
private:
    Rank _size{};     //定义大小（目前存储的元素的个数）
    int _capacity{};    //定义容量
    T *_elem;   //定义元素空间
protected:


public:
    void copyFrom(T *A, Rank lo, Rank hi);  // 复制函数

    void expand();  // 拓展空间

    ~vector(); // 释放空间

    explicit vector(int c = DEFAULT_CAPACITY); //初始化一个向量
    vector(T *A, Rank lo, Rank hi) {
        copyFrom(A, lo, hi);  // 从一个数组数组中去复制
    }

    vector(vector<T> const &v, Rank lo, Rank hi) {
        copyFrom(v._elem, lo, hi);  // 从一个向量中去复制
    }

    vector(vector<T> const &v) {
        copyFrom(v._elem, 0, v._size); // 复制一个向量
    }

    T &operator[](Rank r) const { return _elem[r]; } //重载操作符[]，使得向量可以直接通过下标进行访问。

    Rank insert(Rank r, T &e); // 添加元素

    int remove(Rank lo, Rank hi); // 删除区间 返回区间长度

    T remove(Rank r); // 删除元素，获取返回的元素

    Rank find(T const &e, Rank lo, Rank hi); // 查找元素，返回元素的位置。

    int deduplicate();

    template<typename VST>
    void traverse(VST &visit) {
        for (int i = 0; i < _size; i++) {
            visit(_elem[i]);
        }
    }

    struct Increase {
        virtual void operator()(T &e) { ++e; }
    };

    void increase(vector<T> &V) {
        V.traverse(Increase());
    }
    // 传入一个函数进去进行依次操作。

    // 有序向量部分
    int disordered();

    int uniquify();

    Rank search(int e, Rank lo, Rank hi);

    Rank binarySearch(T *A, T &e, Rank lo, Rank hi);

    Rank FibonacciSearch(T *A, T &e, Rank lo, Rank hi);

    Rank InterpolationSearch(T *A, T &e, Rank lo, Rank hi);

    void sort(Rank lo, Rank hi);

    void bubblesort(Rank lo, Rank hi);

    Rank bubble(Rank lo, Rank hi);

    int getsize() { return _size; }

    void mergesort(Rank lo, Rank hi);

    void merge(Rank lo, Rank mi, Rank hi);
};
template<typename T>
void vector<T>::merge(Rank lo, Rank mi, Rank hi) {
    T * A = _elem + lo; // 从lo开始得到我们的中心数组
    int left = mi - lo;  // 获得区间长度
    T * B = new T[left]; // 创造空间
    for (int i = 0; i < left; i ++) {
        B[i] = A[i]; // 转移复制
    }
    T * C = _elem + mi; // 创建C指针
    int right = hi - mi; // 获得右区间长度
    for  (Rank m = 0, j = 0, k = 0; j < left;) { // 无需考虑C到达右侧区间， 只需要关注B是否到达了右侧，如果到达了的话就直接终止。
        if ((j < left) && ( B[j] <= C[k])) {
            A[m++] = B[j++];
        }
        if ((left <= j) || (C[k] < B[j])) {
            A[m++] = C[k++];
        }
    }
    delete [] B;
}

template<typename T>
void vector<T>::mergesort(Rank lo, Rank hi) {
    if ((hi - lo) < 2) return;
    Rank mi = (lo + hi) / 2; // 找到中间值
    mergesort(lo, mi);  // 排序
    mergesort(mi, hi); // 排序
    merge(lo, mi, hi); // 合并
}







// Bubble算法1.0
//template<typename T>
//bool vector<T>::bubble(Rank lo, Rank hi) {
//    bool sorted = true;
//    if (lo == 0) { lo = 1; }
//    while (lo < hi) {
//        if (_elem[lo - 1] > _elem[lo]) {
//            sorted = false;
//            swap(_elem[lo - 1], _elem[lo]);
//        }
//        lo++;
//    }
//    return sorted;
//}
//
//template<typename T>
//void vector<T>::bubblesort(Rank lo, Rank hi) {
//    while (!bubble(lo, hi--)) {}
//}

//bubble算法2.0
template<typename T>
void vector<T>::bubblesort(Rank lo, Rank hi) {
    while (lo < (hi = bubble(lo, hi))) {}
}

template<typename T>
Rank vector<T>::bubble(Rank lo, Rank hi) {
    Rank last = lo;
    while (++lo < hi) {
        if (_elem[lo - 1] > _elem[lo]) {
            last = lo; // 记录逆序对的右侧为last
            swap(_elem[lo - 1], _elem[lo]); // 交换两项
        }
    }
    return last;
}

template<typename T>
void vector<T>::sort(Rank lo, Rank hi) {
    mergesort(lo, hi);
}

// 插值查找: 类似于字典的查找方式，指查找均匀独立的分布去查找。但是当数据出现扰动的时候效率就会很低。
template<typename T>
Rank vector<T>::InterpolationSearch(T *A, T &e, Rank lo, Rank hi) {
    Rank mi = lo + (hi - lo) * (e - A[lo]) / (A[hi] - A[lo]);
    if (e < A[lo] || e >= A[hi]) return -1;
    while (lo < mi) {
        (e < A[mi]) ? hi = mi : lo = mi + 1;
        mi = lo + (hi - lo) * (e - A[lo]) / (A[hi] - A[lo]);
    }
    return lo;
}

template<typename T>
Rank vector<T>::FibonacciSearch(T *A, T &e, Rank lo, Rank hi) {
    while (lo < hi) {
        int mi = 3 * (lo + hi) / 5;
        if (A[mi] < e) {
            lo = mi + 1;
        } else if (e < A[mi]) {
            hi = mi;
        } else {
            return mi;
        }
    }
    return -1;
}
// BinarySearch 1
//template<typename T>
//Rank vector<T>::binarySearch(T *A, T &e, Rank lo, Rank hi) {
//    while (lo < hi) {
//        int mi = (lo + hi) / 2;
//        if (A[mi] < e) {
//            lo = mi + 1;
//        } else if (e < A[mi]) {
//            hi = mi;
//        } else {
//            return mi;
//        }
//    }
//    return -1;
//}

//template<typename T>
//Rank vector<T>::binarySearch(T *A, T &e, Rank lo, Rank hi) {
//    int mi;
//    while (1 < hi - lo) {
//        mi = (hi + lo) / 2;
//        (A[mi] < e) ? lo = mi : hi = mi;
//    }
//    return (e == A[mi]) ? mi : -1;
//}

template<typename T>
Rank vector<T>::binarySearch(T *A, T &e, Rank lo, Rank hi) {
    Rank mi = 0;
    while (lo < hi) {
        mi = (lo + hi) / 2;
        (e < A[mi]) ? hi = mi : lo = mi + 1;
        /*
         * 区间压缩理解：
         *  1. 当满足e < A[mi] 时候，也就是说mi那个位置是严格大于我们的e的，也就是直接压缩过来
         *  2. 当不满足 e < A[mi] 的时候， 也就是说，mi那个位置一定是小于等于e的，那么我们就需要把这个区间往mi的右侧压缩
         *  如果等于e，那么往右压缩可以跳出重复项，如果不等于而是小于，那么就更加显然了，肯定得右移，如此以往最后得到的就是
         *  大于等于e的最右边的一个值，右边就是刚好大于e的值，而此时的lo是和hi相互重合的一个，往左走一格就是那个刚刚好小于e的位置
         *  然后返回值就是 --lo
        */
    }
    return --lo;
}

template<typename T>
Rank vector<T>::search(int e, Rank lo, Rank hi) {
    // 返回这个binarySearch的返回值。
    return binarySearch(_elem, e, lo, hi);
}

template<typename T>
int vector<T>::uniquify() {
    int oldSize = _size;
    int i = 0; // 从一号元素开始查重
    // 注意这里是正对有序向量而言的唯一化
    int j = 0;
    while (++j < _size) {
        if (_elem[i] < _elem[j]) {
            remove(i + 1, j); // 删除掉这个区间的量， 但是我们还可以使用赋值去默认删除。
            i = j;
        }
    }
    return oldSize - _size;
}


template<typename T>
int vector<T>::disordered() {
    int count = 0;
    int i = 1;  // 开始阶段
    while (i < _size) {
        count += (_elem[i - 1] >= _elem[i]);
        i++;
    }
    return count;
}

template<typename T>
int vector<T>::deduplicate() {
    // 在定义一个区间后在原先的区间去查找，如果找到了，就使用remove去掉这个元素，没有的话就往下去寻找。
    // 返回值是删除的重复元素的个数
    int oldSize = _size; // 记录下oldSize
    Rank i = 1;  // 从i=1开始查找。
    while (i < _size) { // 知道检测到最后一个元素
        (find(_elem[i], 0, i) >= 0) ? remove(i) : i++;
        // 如果数据合法的话就返回的秩是大于lo的，那么也就是说 >= 0 那么就找到了重复的数，那么remove（i）,否则就i ++
    }
    return oldSize - _size;  // 返回差值， 返回这个重复的元素的个数。

}

template<typename T>
Rank vector<T>::find(const T &e, Rank lo, Rank hi) {
    while (lo < hi-- && _elem[hi] != e) {
        // 先判断lo 小于 hi ，然后hi --
        // 逐个扫描
    }
    return hi;  // 找到了 返回 hi。 // 如果合法的话就是我们的真实的秩，如果不是合法的话就返回一个小于lo 的函数
}

template<typename T>
T vector<T>::remove(Rank r) {
    T e = _elem[r]; // 备份一份元素以便于等会儿返回
    remove(r, r + 1);
    return e;
    // 颠倒过来使用单个元素去达到删除区间的作用是很不合理的
    // 每每调用一次删除元素，后面的元素都需要往前移动一位，这样就造成了复杂度的攀升
    // 因此我们应当使用区间删除去对应的做到删除元素的功能。
}

template<typename T>
int vector<T>::remove(Rank lo, Rank hi) {
    if (hi == lo) { return 0; }
    while (hi < _size) {
        _elem[lo++] = _elem[hi++];
        // 赋值操作 一定得是从低位赋值开始，
        // 如果不是从低位开始，就容易出现我们高位数覆盖掉lo以下的数字，
        // 使用hi ++ 限定条件是 hi < _size 使得我们能够把所有的hi以后的数字完全遍历到，并且赋值成功。
    }
    _size = lo;   // 按理来说应该是 _size = _size - (hi‘ - lo’) 而这里的hi‘已经等于_size了， 而 lo' 已经变成了数组的长度
    return (hi - lo);  // 返回区间的长度
}

template<typename T>
void vector<T>::copyFrom(T *A, Rank lo, Rank hi) {
    _size = 0;
    _elem = new T[2 * (hi - lo)];
    while (lo < hi) {
        _elem[_size++] = A[lo++];
    }
}

template<typename T>
void vector<T>::expand() {
    if (_size < _capacity) {
        return; // 如果说内部的存储量小于_capacity,则直接返回.
    }
    _capacity = max(_capacity, DEFAULT_CAPACITY);
    T *oldElem = _elem; // 指向老指针中的元素
    _elem = new T[2 * _capacity]; // 扩大容量
    // 转移操作
    for (int i = 0; i < _size; i++) {
        _elem[i] = oldElem[i];
        // 为什么oldElem中可以放下呢，这是由于传入的_elem其实是一个类似于数组的东西，
        // 如果不能就早就Significant Fault
        // 而我们不确定这个放入构造的向量能否存起来这么些数据。
    }
    delete[] oldElem; // 释放
}

template<typename T>
vector<T>::~vector() {
    delete[] _elem;
}

template<typename T>
vector<T>::vector(int c) {
    _elem = new T[_capacity = c];
    _size = 0;
}

template<typename T>
Rank vector<T>::insert(Rank r, T &e) {
    expand();  // 检查是否出现了溢出
    for (int i = _size; i > r; i--) {
        _elem[i] = _elem[i - 1];  //从大到小的去检查，方便我们数据的保留，不能丢失
    }
    _elem[r] = e; // 把空出来的r号元素输入
    _size += 1; // 长度增加
    return r; // 返回一个值为对应的值。
}

#endif //DATA_STRUCTURE_AND_ALOGTHM_VECTOR_H

数据结构与算法

绪论

算法

好算法

计算模型

Turing Machine（图灵机）

RAM: Random Access Machine

大o记号

渐进分析法： 大o记号

算法分析

级数

循环

冒泡排序

封地估算

迭代与递归

迭代

递归方程

数组倒置

二分递归

动态规划

向量(Vector)

向量ADT

可扩充向量

静态空间管理策略

动态空间管理策略

扩容方法

递增式扩容

加倍扩容

分摊复杂度

无序向量

元素访问

插入

区间删除

单元素删除

查找

唯一化

遍历操作

有序向量

有序性

唯一化

二分查找

FibonacciSearch

向量完全体

渐进分析法：大o记号